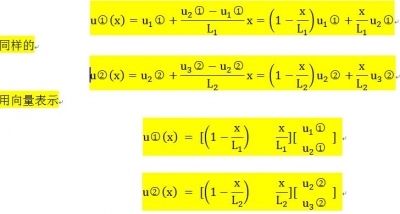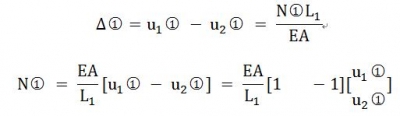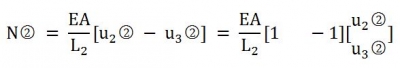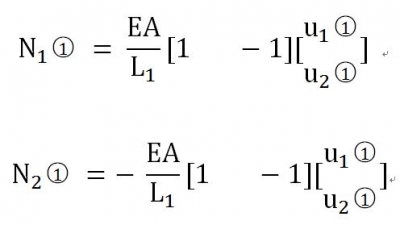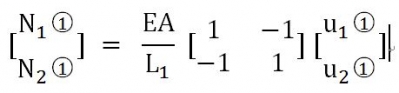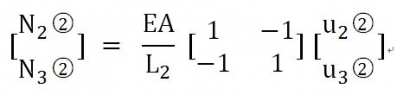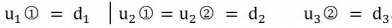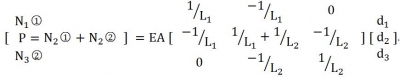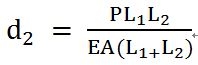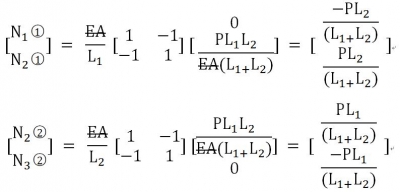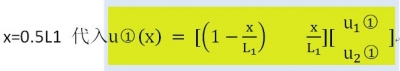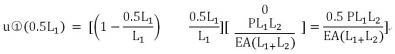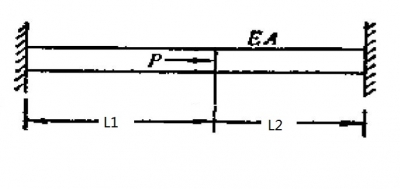
假設(shè)一均勻直桿，彈性模量E，截面積A，長(zhǎng)度2L兩端固定，在中間位置施加一向右的載荷P，求直桿內(nèi)應(yīng)力。

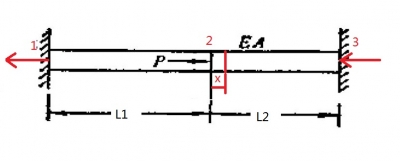
材料力學(xué)解法：假設(shè)P的作用點(diǎn)發(fā)生了一微小位移X

求解完畢。

有限元解法思路：

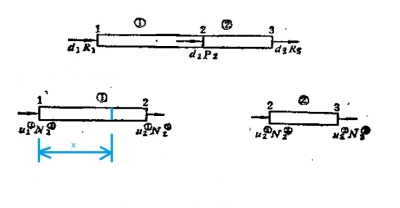
將直桿劃分為2個(gè)單元，用這連個(gè)離散單元的組合來(lái)逼近連續(xù)體直桿，設(shè)單元編號(hào)，結(jié)點(diǎn)編號(hào)1，2，3，單元上軸向位移與軸向內(nèi)力如上圖 u表示結(jié)點(diǎn)位移 N表示結(jié)點(diǎn)內(nèi)力。

假設(shè)x為單元 內(nèi)任意一點(diǎn)則位移表達(dá)式為（以下的位移表達(dá)式為假設(shè)的，其實(shí)就是有限元中的單元形函數(shù)）

根據(jù)胡克定律，對(duì)于單元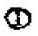，由軸向力引發(fā)的位移

同樣對(duì)于單元                    

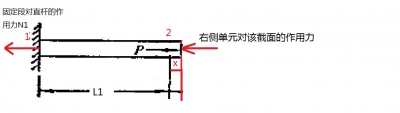
對(duì)單元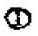，受力分析得出結(jié)點(diǎn)的受力情況

將上述單元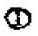的結(jié)點(diǎn)受力表達(dá)式寫(xiě)成矩陣結(jié)構(gòu)

同樣的方式針對(duì)單元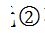，那么單元2 的結(jié)點(diǎn)受力表達(dá)式的矩陣結(jié)構(gòu)是

單元的剛度可表示為

在結(jié)點(diǎn)2處的平衡條件      

各結(jié)點(diǎn)的位移連續(xù)條件   

單元的剛度矩陣方程可以組合到如下形式（整體剛度矩陣方程）

可寫(xiě)成如下形式  P = Kd         K ———— 結(jié)構(gòu)總剛度矩陣    d ———— 結(jié)構(gòu)結(jié)點(diǎn)位移向量   P ———— 結(jié)構(gòu)結(jié)點(diǎn)載荷向量

邊界條件   d1=d3 =0   代入求得

帶入各單元內(nèi)力方程

到現(xiàn)在位置我們并沒(méi)有使用黃色背景部分的公式，它起什么作用呢？目前我們能得到的是各結(jié)點(diǎn)的位移，各點(diǎn)的受力，以及桿的內(nèi)力及內(nèi)應(yīng)力（此時(shí)因?yàn)閭€(gè)單元內(nèi)部的應(yīng)力處處相等），那如何求得單元內(nèi)部各處的位移呢？那就得使用黃色部分的內(nèi)容了。比如單元中間位置發(fā)生的位移是多少

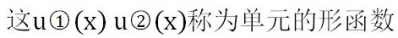，它不僅可以用作單元的內(nèi)插值函數(shù)，即把單元內(nèi)任意一點(diǎn)的位移用結(jié)點(diǎn)位移表示，而且可作為加權(quán)余量法中的加權(quán)函數(shù)，可以處理外載荷，將分布力等效為結(jié)點(diǎn)上的集中力和力矩，此外可用于等參單元的坐標(biāo)變換。