|
發(fā)布時間: 2019-6-12 09:18
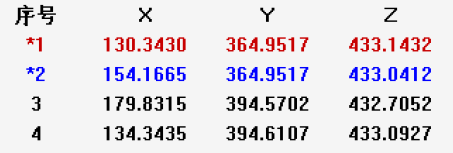
正文摘要:本帖最后由 wryp 于 2019-6-12 10:57 編輯 比如說有四個點,坐標分別如下: 我想知道的是,這個時候怎樣評價這四個點所在平面的平面度? 謝謝諸位! ... |
|
平面度 你只需要看Z軸就行,從Z軸的數(shù)據(jù)看差值即可 |
| HAOGAOSHENG |
鋤頭雨 發(fā)表于 2020-9-21 09:22 完全同意!特別是最后一段話! |
本帖最后由 鋤頭雨 于 2020-9-21 09:27 編輯 wryp 發(fā)表于 2020-9-19 09:53 首先,樓主的方法是根據(jù)測試點構造一個凸面體,然后求頂點到平面法向高度的最大值,這種方法的結果除少數(shù)情況下,一定會比最小二乘法和最小區(qū)域法大,具體大多少不確定。但滿足樓主的方法的結果也肯定能夠滿足其他兩種方法。 最小二乘法就是通過最小二乘法擬合出一個平面,平面兩側點到這個平面距離最大值之和就是平面度誤差。 最小二乘法擬合面的幾何意義可以這么理解:找到一個平面,使所有數(shù)據(jù)點到該平面的距離之和最小(殘差最小)。具體的算法百度或者知網(wǎng)就可以,關鍵詞最小二乘法;平面度。 最小區(qū)域法是:找到相距最小的兩平行平面,使所有測量點包含在兩平面之間。可以參考JJG 117-2013 《平板檢定規(guī)程》或者知網(wǎng),關鍵詞最小區(qū)域法法;平面度。 二者原理不同,這也就是上面那位老哥說的最小二乘法的計算結果一般比最小區(qū)域法大的原因。 另外,我認為平面度就是用來控制平面的,和基準無關。控制平面在空間中的幾何坐標和角度的應該是尺寸公差和位置公差。 |
點點人生123 發(fā)表于 2020-9-20 18:41 您是對的!非常感謝! |
wryp 發(fā)表于 2020-9-20 17:54  我說的基準是帶引號的老板,這個基準就是理想平面,理想平面都沒有,假如四個點都歪到姥姥家去了但是它們在一個面上,比如整個面都斜了45度 這個時候就算平面度是0也沒有意義呀,wryp 發(fā)表于 2020-9-20 17:54 我說的基準是帶引號的老板,這個基準就是理想平面,理想平面都沒有,假如四個點都歪到姥姥家去了但是它們在一個面上,比如整個面都斜了45度 這個時候就算平面度是0也沒有意義呀,wryp 發(fā)表于 2020-9-20 17:54以后不懂不要亂發(fā)言!不發(fā)言不會曝露自己的水平! |
點點人生123 發(fā)表于 2020-9-20 17:41 以后不懂不要亂發(fā)言!不發(fā)言不會曝露自己的水平! |
| 樓主對平面度理解有誤吧,“基準”都沒有,光四個點比較有什么意義 |
本帖最后由 wryp 于 2020-9-19 09:56 編輯 鋤頭雨 發(fā)表于 2020-9-18 16:45 感謝對這個問題的關注! 我用三坐標時,選擇的是最小二乘法。 我不清楚的是:三樓我根據(jù)平面度的定義手工算的結果對不對? 然后是最小二乘法是怎么處理測量的數(shù)據(jù)的?能不能把算法告訴我? 謝謝! |
Archiver|手機版|小黑屋|機械社區(qū) ( 京ICP備10217105號-1,京ICP證050210號,浙公網(wǎng)安備33038202004372號 )
GMT+8, 2025-7-26 15:03 , Processed in 0.087265 second(s), 21 queries , Gzip On.
Powered by Discuz! X3.5 Licensed
© 2001-2025 Discuz! Team.